Module 4 Understanding shape
Select each tab to find out more or use the breadcrumb trail to go to another part of this resource.
Can I calculate angles on a straight line and in a triangle?

Example review questions

  • Calculate the missing angle.
    180 degree angle split into two smaller angles. One angle is 72 degrees. The other angle has a question mark inside it.
  • If one angle in a triangle measures 70° and another measures 65°, what does the third angle measure? How do you know?
  • Calculate the missing angles shown as question marks on this diagram of an equilateral triangle. Explain how you did it.
    Equilateral triangle on a flat plain. To the left of the triangle is a semi circle which forms angle with the side of the triangle.

Teaching guidance

This teaching guidance document suggests some of the key vocabulary, models, images and practical equipment that children should experience and be able to use. It also includes some teaching tips to provide a few starting points for ways of supporting children with this area of mathematics.

PDF file Can I calculate angles on a straight line and in a triangle? - teaching guidance | 35KB new window

Consolidation and practice

These resources are to support children in guided or independent work. Roll over the highlighted resources for a description.

PDF file How to use calculating angles ITP | 150KB new window

SWF file Calculating angles ITP | 45KB new window

PDF file How to use fixing points ITP | 133KB new window

SWF file Fixing points ITP | 55KB new window

PDF file Springboard 6, Lesson 14 Calculate angles in a triangle and around a point | 58KB new window

PDF file Springboard 6, Lesson 14 Resources | 20KB new window

PDF file Springboard 7, Unit 14, Section 5 Calculations involving angles | 1.1MB new window

Calculating angles

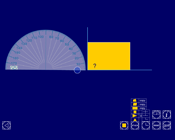
itp_calculating_angles.png

This interactive teaching program (ITP) is an ICT-based tool to support the exploration of angles. Calculating angles ITP allows the child or teacher to represent single or multiple shapes rotated around a central point in one, two or four quadrants. The size of angles can be estimated or calculated and confirmed using the on-screen protractor or reveal function.

Fixing points

itp_fixing_points.png

This interactive teaching program (ITP) is an ICT-based tool to support the exploration of shape and space. Fixing points ITP allows the child or teacher to create one or more shapes by connecting a number of vertices on a grid. Angles can be estimated and measured, and the effect of moving different vertices can be explored.

Opportunities to use and apply

Possible contexts include:

  • using ICT software to create triangles.
  • investigations, e.g. How can all quadrilaterals be divided into two triangles, and how can this knowledge be used to calculate the sum of the internal angles in a quadrilateral?
  • mental calculation, e.g. Two angles of a triangle are 43º and 57º, what is the third angle?
 

Confirming learning

Ask probing questions such as:

  • Ashley measured the angles in a triangle. He said: ‘The angles are 30°, 60° and 100°.’ Could he be correct? Why?
  • Explain why a triangle cannot have an internal angle of 185°.
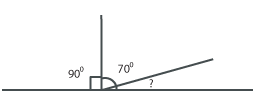
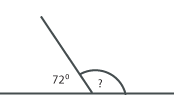
  • How would you calculate the missing angle?
    180 degrees split into three: 90 degrees, 70 degrees and a question mark.
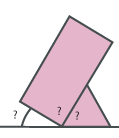
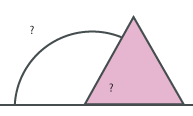
  • What are the three angles indicated by question marks on this diagram showing a rectangle and equilateral triangle? How do you know?
    A diagram composed of a number of different shapes, creating angles.