Module 4 Understanding shape
Select each tab to find out more or use the breadcrumb trail to go to another part of this resource.
Can I use coordinates to draw, locate and complete shapes?

Example review questions

  • Why is the point (4, 1) not the same as (1, 4)? Can you draw a diagram to explain?
  • Three of the four vertices of a square are (3, 10), (5, 12) and (7, 10). Work out the coordinates of the fourth vertex.
  • These points are the coordinates of the vertices of a shape: (1, 5), (2, 5), (4, 3), (2, 1), (1, 1).
    What is the name of the shape?
  • Tell me four coordinates that could be the vertices of a rectangle.

Teaching guidance

This teaching guidance document suggests some of the key vocabulary, models, images and practical equipment that children should experience and be able to use. It also includes some teaching tips to provide a few starting points for ways of supporting children with this area of mathematics.

PDF file Can I use coordinates to draw, locate and complete shapes? - teaching guidance | 40KB new window

Consolidation and practice

These resources are to support children in guided or independent work. Roll over the highlighted resource for a description.

DOC file How to use coordinates ITP | 184KB new window

SWF file Coordinates ITP | 69KB new window

PDF file Springboard 7, Unit 8, Sections 2 and 3 Triangles and coordinates, Fun with coordinates | 824KB new window

Coordinates

itp_coordinates.png

This interactive teaching program (ITP) is an ICT-based tool to support the exploration of coordinates. Coordinates ITP allows the child or teacher to use a marker to identify the coordinates of points on different grids, mark points and draw lines and shapes, working in one, two or four quadrants to introduce both positive and negative coordinates. The ITP can also be used to explore the properties of 2-D shapes and to predict translations, rotations and reflections of various shapes in the different quadrants.

Opportunities to use and apply

Possible contexts include:

  • finding all possibilities, e.g. If (6, 5) and (8, 5) are two vertices of a square, how many possibilities are there for the pair of missing vertices? What are they?
  • geography, e.g. Identifying and recording references for where children live, and other features of their locality, on a map.
  • reflection and translation, e.g. Sketch the reflection or translation of a shape and record its new coordinates. Use this to predict the coordinates of the shape if it were reflected or translated again.

Confirming learning

Ask probing questions such as:

  • Here is a shaded square.

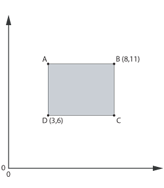
    A diagram consisting of a square situated within a graph. The square has four labelled corners: A in top left, B in the top right, C in the bottom right and D in the bottom left. Corner B has eight, 11 as its coordinates. Corner D has three, six as its coordinates. A and C do not have any coordinates.

    Write the coordinates for point A and point C. Explain how you worked them out. Did you annotate the diagram? How did his help? If you reflected the square along the side BC what would the new coordinates of the vertices of the square be?
  • Three of the four vertices of a square are (3, 10), (5, 12) and (7, 10). Work out the coordinates of the fourth vertex.
  • What could the coordinates be for a square with sides that are not parallel or perpendicular to the axes?