Module 3 Calculating
Select each tab to find out more or use the breadcrumb trail to go to another part of this resource.
Can I divide a two-digit number by a one-digit number and explain any remainders?

Example review questions

  • Mary wants to make 60p using 5p coins. How many will she need? How do you know?
  • If you put 72 cubes into boxes that hold five cubes, how many boxes would you need? Explain why.
  • How many 3p lollies can you buy with 45p? Record your method.
  • How does knowing that 10 × 3 = 30 and 4 × 3 = 12 help you know how many threes there are in 42?
  • How many 19p pencils can I buy with 60p? How much change will I get? Record your working.
  • What is 47 ÷ 4?

Teaching guidance

This teaching guidance document suggests some of the key vocabulary, models, images and practical equipment that children should experience and be able to use. It also includes some teaching tips to provide a few starting points for ways of supporting children with this area of mathematics.

DOC file Can I divide a two-digit number by a one-digit number and explain any remainders? - teaching guidance | 187KB new window

Consolidation and practice

These resources are to support children in guided or independent work. Roll over the highlighted resources for a description.

PDF file How to use grouping ITP | 157KB new window

SWF file Grouping ITP | 20KB new window

PDF file How to use remainders after division ITP | 184KB new window

SWF file Remainders after division ITP | 29KB new window

XLS file Multiplication and division with partitioning | 37KB new window

DOC file Number line division teaching prompts | 37KB new window

Grouping

itp_grouping.png

This interactive teaching program (ITP) is an ICT-based tool to support the exploration of division. Grouping ITP allows the child or teacher to model division as grouping and to link this process to jumps on a number line. It can also be used to introduce children to remainders and to apply their knowledge through setting similar problems that can be solved using the image displayed.

Remainders after division

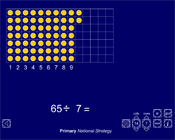
itp_remainders_after_division.png

This interactive teaching program (ITP) is an ICT-based tool to support the exploration of number and calculation. Remainders after division ITP can be used to demonstrate division as grouping, and to develop children's understanding of remainders and the notation for division. Keeping the number of counters fixed but changing the number of rows demonstrates the effect of changing the divisor in the calculation. Children can explore the effect different divisors have on the remainder.

Opportunities to use and apply

Possible contexts include:

  • word problems involving money and measures, e.g. How many 2p coins would you need to make 32p?
  • patterns and puzzles, e.g. When a number is divided by five it gives a remainder of two. Tell me three different numbers between 10 and 30 that it could be.
  • 48 ÷ circle gives an answer with no remainder. Which one-digit numbers could go in the circle?
  • problems from the PDF file Mathematical challenges booklet | 920KB new window, e.g. problems 30 and 38.
 

Confirming learning

Ask probing questions such as:

  • Work out the missing number: Emtpy box × 2 = 56
  • How does knowing that 10 × 6 = 60 help you to calculate the answer to 72 ÷ 6?
  • Make up some division questions that have no remainder. How did you do this? How did you know they don’t have a remainder? Make up some division questions that have a remainder of one. How did you do it?
  • Jack says that 71 ÷ 4 = 17 remainder 5. Can he be correct?