Module 6 Handling data
Select each tab to find out more or use the breadcrumb trail to go to another part of this resource.
Can I use the 0-1 probability scale to measure the probabilities of outcomes?

Example review questions

  • Imagine rolling a normal 1–6 dice. Mark on the scale below the probability of:
    1. rolling a 5
    2. rolling a number greater than 2
    3. rolling a zero
    4. rolling an odd number
    Which example gives the probability closest to 1? Explain why.
    Seven point scale from zero to one.
    Make a statement in which the probability is: 1; 1/3; 5/6
  • I have a 6-sided dice numbered 1–6 and an 8-sided dice numbered 1–8.
    Use the probability scale to illustrate and compare the chance of getting a 6 on the 6-sided dice with the chance of getting a 6 on the 8-sided dice. What about getting an even number, or a multiple of 4?
    Probability scale showing zero, half and one with zero labelled as impossible and one labelled as certain.
  • Decide whether the chance of landing on green is greater than, less than or equal to 1/2 for each spinner. Explain your answers.
    Scale showing zero as impossible, half as even and one as certain.

Teaching guidance

This teaching guidance document suggests some of the key vocabulary, models, images and practical equipment that children should experience and be able to use. It also includes some teaching tips to provide a few starting points for ways of supporting children with this area of mathematics.

PDF file Teaching guidance: Can I use the 0–1 probability scale to measure the probabilities of outcomes? | 88KB new window

Consolidation and practice

These resources are to support children in guided or independent work. Roll over the highlighted resource for a description.

PDF file How to use number spinners ITP | 139KB new window

SWF file Number spinners ITP | 38KB new window

XLS file Probability spreadsheet | 89KB new window

DOC file How to get more pupils from level 3 to level 5 – Snappers 15 | 91KB new window

Visit the nrich website new window for further activities to support practice and application.

Number spinners

itp_number_spinners.png

This interactive teaching program (ITP) is an ICT-based tool to support the exploration of number, reasoning and problem solving. Number spinners ITP allows the child or teacher to generate 3, 4, 5 or 6 random numbers on up to 3 spinners. Numbers from 0 to 99 can be displayed.

Opportunities to use and apply

Possible contexts include:

  • Games, e.g. Probability based game shows such as 'Play your cards right'; card and dice games, for example: Use two 1–6 dice. Player A wins a point if the numbers on the two dice total 2, 3, 4, 5, 10 or 12. Player B wins a point if the numbers total 6, 7, 8 or 9. Is this fair? Explain your answer. If the game is not fair, devise new fair rules.
  • 3-D shape, e.g. Use nets of regular polyhedra, to make dice. Ask the children to compare the likelihood of getting a particular number with different shapes and explain their conclusions.
  • Problems, e.g. Colour a spinner so that it is twice as likely to land on green as it is to land on blue. Justify why you think your shading represents the given probability. Use the language of probability and the probability scale to justify your answer.

 

Confirming learning

Ask probing questions such as:
  • Decide whether each statement is true or false. Explain how you know. Use the probability scale to illustrate your explanation.
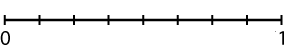
    Nine point scale of zero to 1 with A, B, C labels.
    Five spinners. Spinner A in two halves, labelled one and two. Spinner B in four parts, labelled one, three, two and two. Spinner C in eight parts, labelled one, five, three, four, one, two, one and six. Spinner D in two parts, labelled one and three.
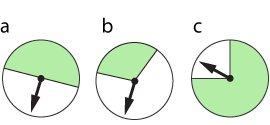
    • Spinners A, B & C are equally likely to spin a 2.
    • The chance of spinning a 3 on spinner B and on spinner C is equal.
    • You would be more likely to spin a 1 on spinner D than on any other.
    • There is a 25% chance of getting a 3 on spinner C.
    • You are more likely to spin an odd number on spinner C than any other.
    • The chance of spinning a number greater than 4 on spinner C is 2/6.
  • A fair dice has the numbers 1, 3, 3, 3, 4 and 4 on it. Draw your own probability scale and mark the probability of rolling: 2; 3; 4; a number smaller than 10.