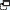Module 4 Understanding shape
Select each tab to find out more or use the breadcrumb trail to go to another part of this resource.
Can I use my understanding of angles and shapes to work out missing angles?

Example review questions

  • A triangle has one angle of 55° and one of 78°. How big is the third angle?
  • Look at this diagram.
    Diagram showing one angle of fifty five degrees, the second of seventy eight degrees and the third one unknown
    Work out the size of angle a and angle b without using a protractor.
  • What is the angle between the hour hand and the minute hand of a clock at 7 o'clock? Explain how you worked this out.
  • Work out the missing angles in this kite:
    Kite showing one angle of ninety five degrees, the second of fifty one degrees, and the third and fourth unknown

Teaching guidance

This teaching guidance document suggests some of the key vocabulary, models, images and practical equipment that children should experience and be able to use. It also includes some teaching tips to provide a few starting points for ways of supporting children with this area of mathematics.

PDF file Teaching guidance: Can I use my understanding of angles and shapes to work out missing angles? | 64KB new window

Consolidation and practice

These resources are to support children in guided or independent work. Roll over the highlighted resources for a description.

PDF file How to use calculating angles ITP | 150KB new window

SWF file Calculating angles ITP | 45KB new window

PDF file How to use polygon ITP | 176KB new window

SWF file Polygon ITP | 176KB new window

PDF file How to use fixing points ITP | 31KB new window

SWF file Fixing points ITP | 133KB new window

PDF file Springboard 6 lesson 14 | 57KB new window

PDF file Springboard 6 lesson 14 resource | 19KB new window

Visit the nrich website new window for further activities to support practice and application.

Calculating angles

itp_calculating_angles.png

This interactive teaching program (ITP) is an ICT-based tool to support the exploration of angles. Calculating angles ITP allows the child or teacher to represent single or multiple shapes rotated around a central point in one, two or four quadrants. The size of angles can be estimated or calculated and confirmed using the on-screen protractor or reveal function.

Polygon

itp_polygons.png

This interactive teaching program (ITP) is an ICT-based tool to support the exploration of shape, space and measure. Polygon ITP allows the child or teacher to represent regular polygons with three to ten sides. The ITP can then be used to explore the properties of regular and irregular shapes by dragging vertices and creating additional vertices. The ITP includes an on-screen protractor and ruler.

Fixing points

itp_fixing_points.png

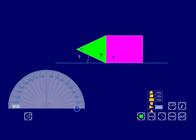
This interactive teaching program (ITP) is an ICT-based tool to support the exploration of shape and space. Fixing points ITP allows the child or teacher to create one or more shapes by connecting a number of vertices on a grid. Angles can be estimated and measured, and the effect of moving different vertices can be explored.

Opportunities to use and apply

Possible contexts include:

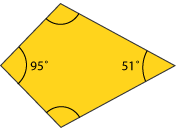
  • Investigating shape properties, e.g. Find the sum of the internal angles of 2-D shapes such as triangles, quadrilaterals, pentagons. What patterns do you notice? Does it matter whether the shapes are regular?
  • Investigating general statements, e.g. When a shape is enlarged its angles do not change; triangles can have 0, 1, 2 or 3 obtuse angles – true or false?
  • Drawing shapes accurately, e.g. Draw a rhombus with side length of 5 cm and two angles of 125°.
  • Using ICT, e.g. use your knowledge of angles to draw an equilateral triangle using software.

Confirming learning

Ask probing questions such as:

  • Sketch an isosceles triangle with an angle of 40° and work out the size of the other angles. Try to find more than one way to do this.
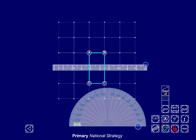
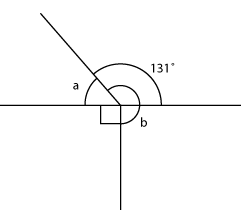
  • Work out the sizes of angles a, b and c.
    Triangle with known angles thirty degrees and forty degrees. Angles a, b and c unknown.
  • How many degrees does the minute hand of a clock turn between 9 am and 11:55 am on the same day? Explain how you worked this out.
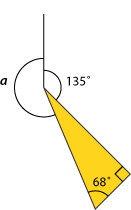
  • Find angle a by marking known angles onto the diagram.
    Line and triangle showing one hundred and thirty five degrees and sixty eight degrees. Angle a unknown.