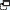Module 4 Understanding shape
Select each tab to find out more or use the breadcrumb trail to go to another part of this resource.
Can I use the language perpendicular and parallel to classify, describe and draw shapes and lines?

Example review questions

  • Here is a shape on a square grid.
    Shape on a square grid

    For each sentence, put a tick (tick.png) if it is true.
    Put a cross (cross.png) if it is not true.

    • Angle C is an obtuse angle.
    • Angle D is an acute angle.
    • Line AD is parallel to line BC.
    • Line AB is perpendicular to line AD.

    Write your own true sentence about the shape using perpendicular.

  • Using dotty paper, draw quadrilaterals with:
    • only one pair of parallel sides
    • only one pair of perpendicular sides
    • two pairs of parallel sides
  • Visualise a hexagonal prism where the hexagonal faces are regular. How many pairs of parallel faces does it have?

Teaching guidance

This teaching guidance document suggests some of the key vocabulary, models, images and practical equipment that children should experience and be able to use. It also includes some teaching tips to provide a few starting points for ways of supporting children with this area of mathematics.

PDF file Teaching guidance: Can I use the language perpendicular and parallel to classify, describe and draw shapes and lines? | 78KB new window

Consolidation and practice

These resources are to support children in guided or independent work. Roll over the highlighted resources for a description.

PDF file How to use coordinates ITP | 184KB new window

SWF file Coordinates ITP | 69KB new window

PDF file How to use polygon ITP | 176KB new window

SWF file Polygon ITP | 176KB new window

PDF file How to use fixing points ITP | 31KB new window

SWF file Fixing points ITP | 133KB new window

PDF file How to use isometric grid ITP | 254KB new window

PDF file Isometric grid ITP | 53KB new window

Visit the nrich website new window for further activities to support practice and application.

Coordinates

itp_coordinates.png

This interactive teaching program (ITP) is an ICT-based tool to support the exploration of coordinates. Coordinates ITP allows the child or teacher to use a marker to identify the coordinates of points on different grids, mark points and draw lines and shapes, working in one, two or four quadrants to introduce both positive and negative coordinates. The ITP can also be used to explore the properties of 2-D shapes and to predict translations, rotations and reflections of various shapes in the different quadrants.

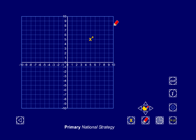
Polygon

itp_polygons.png

This interactive teaching program (ITP) is an ICT-based tool to support the exploration of shape, space and measure. Polygon ITP allows the child or teacher to represent regular polygons with three to ten sides. The ITP can then be used to explore the properties of regular and irregular shapes by dragging vertices and creating additional vertices. The ITP includes an on-screen protractor and ruler.

Fixing points

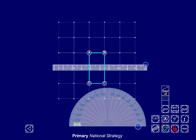
itp_fixing_points.png

This interactive teaching program (ITP) is an ICT-based tool to support the exploration of shape and space. Fixing points ITP allows the child or teacher to create one or more shapes by connecting a number of vertices on a grid. Angles can be estimated and measured, and the effect of moving different vertices can be explored.

Isometric grid

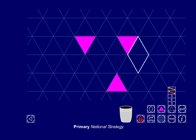
itp_isometric_grid.png

This interactive teaching program (ITP) is an ICT-based tool to support the exploration of shape and space. Isometric grid ITP allows the child or teacher to display equilateral triangles. The grid can be hidden or become an isometric pin board. An 'elastic band' can be stretched around the pins to create outlines. Rhombuses can be selected and dragged to different positions on the grid, and then locked together to form representations of 3-D shapes.

Opportunities to use and apply

Possible contexts include:

  • Art, e.g. Look at pictures by Mondrian and identify parallel and perpendicular lines. Create Mondrian-style pictures given particular criteria.
  • Design technology, e.g. Consider strategies to ensure that adjacent struts in a wooden box frame remain perpendicular.
  • Everyday objects, e.g. Identify parallel and perpendicular lines in everyday objects, e.g. gates, flags.
    Fence showing parallel and perpendicular lines
  • Sorting activities, e.g. classify shapes onto Venn, Carroll and tree diagrams using properties such as has at least one pair of parallel sides/faces.
  • Coordinates, e.g. Draw the straight line between points (1,1) and (6,6). Draw a line perpendicular to this that goes through the point (1,6).

Confirming learning

Ask probing questions such as:

  • Give a time when a clock's minute and hour hands are perpendicular.
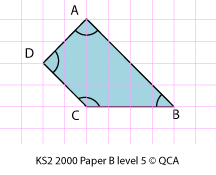
  • Investigate which of these quadrilaterals have diagonals which are perpendicular to each other: square, oblong, kite, parallelogram.
  • Name a 3-D shape that has: only one pair of parallel faces; three pairs of parallel faces; no pairs of parallel faces.
  • Draw a quadrilateral where all touching sides are perpendicular. What is the relationship between opposite sides?
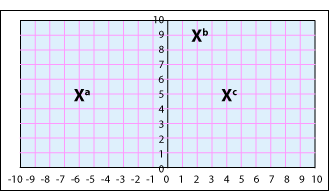
  • Points a, b and c are three of the vertices of a quadrilateral. Give the coordinates of the fourth vertex, if the quadrilateral has: only one pair of parallel sides; two pairs of parallel and perpendicular sides; only one pair of perpendicular sides.
    Points a, b and c as three of the vertices of a quadrilateral