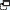Module 1 Counting and understanding number and associated objectives
Select each tab to find out more or use the breadcrumb trail to go to another part of this resource.
Can I solve simple problems involving ratio and proportion?

Example review questions

  • These ingredients are needed to make a banana and berry smoothie for 4 people:
    • 2 bananas
    • 500 ml plain yoghurt
    • 400 g berries
    List the ingredients needed for 6 people.
  • What proportion of the numbers from 1 to 100 inclusive:
    • are multiples of 10?
    • contain the digit 3?
  • A pack of nuts and raisins is made up of 1/3 nuts and the rest raisins. The pack contains 100 g of raisins. How much does the pack weigh altogether?
    Explain how you worked this out.
  • The ratio of a scale model to a real bridge is 1 to 50. The bridge is 425 m long. How long is the model?

Teaching guidance

This teaching guidance document suggests some of the key vocabulary, models, images and practical equipment that children should experience and be able to use. It also includes some teaching tips to provide a few starting points for ways of supporting children with this area of mathematics.

PDF file Teaching guidance: Can I solve simple problems involving ratio and proportion? | 52KB new window

Consolidation and practice

These resources are to support children in guided or independent work. Roll over the highlighted resources for a description.

PDF file How to use ratio and proportion ITP | 51KB new window

SWF file Ratio and proportion ITP | 86KB new window

PDF file Teaching activity using ratio and proportion | 154KB new window

XLS file Pie chart spreadsheet | 39KB new window

PDF file How to use fractions ITP | 86KB new window

SWF file Fractions ITP | 25KB new window

Visit the nrich website new window for further activities to support practice and application.

Ratio and proportion

image alt text here

This interactive teaching program (ITP) is an ICT-based tool to support the exploration of number. Ratio and proportion ITP allows the child or teacher to represent and combine two different liquids in a chosen ratio.

Fractions

image alt text here

The Fractions interactive teaching program (ITP) is an ICT-based tool to support the exploration of part numbers. Fractions ITP allows the child or teacher to represent and compare fractions on fraction strips. The displayed strips can be labelled as a vulgar fraction, a decimal (to three decimal places) or a percentage, and the ratio of yellow to green parts of each strip can also be displayed.

Opportunities to use and apply

Possible contexts include:

  • Geography, e.g. using scale to interpret/draw maps and plans.
  • Design technology/art, e.g. creating scale models or drawings.
  • Food technology, e.g. adapting recipes; proportions of ingredients.
  • Measures, e.g. conversion between units.
  • Data handling, e.g. proportions within pie charts; conversion graphs.
  • Important mathematical ratios, e.g. The Golden Ratio; Pi.

Confirming learning

Ask probing questions such as:

  • Fruit squash is to be mixed with water in the ratio 1:5. How much squash and how much water should be put in to fill a 3 litre jug? How did you work this out?
  • Tina has 440 sweets of which 40 are red. Ryan has 540 sweets of which 45 are red. Who has the greater proportion of red sweets? Explain how you solved this problem.
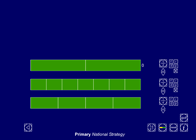
  • In this pie chart, the yellow segment represents 25 children. How many children does the whole pie chart represent?
    A pie chart with one eighth coloured in blue, two eighths coloured in purple and five eighths coloured in yellow.